Mechanical engineering students’ struggles with units of measure
By: Juan C. Morales Brignac, Ph.D., P.E.,
Mechanical Engineering Department Head
Universidad Ana G. Méndez, Gurabo Campus
Abstract
The correct use of units of measure is a critical and fundamental skill that is often taken for granted. The fact that units are taught in high school leads to the expectation that university freshmen master these skills. Unfortunately, faculty often observe that students struggle with units. Although the literature is limited on the nature and extent of students’ struggles with units, it is shown that all of it, without exception, points to a pervasive problem in STEM programs. This paper contributes to the literature by exploring the evolution in the performance of N=21 senior mechanical engineering students enrolled during the Fall 2019 semester in a 3-credit-hour, required course that prepares them for the NCEES Fundamentals of Engineering (FE) Exam. Students were given a unit-conversion quiz at the beginning each class session. It was corrected on the spot, with a score of either 1 or 0, followed by a discussion of the quiz. A score of 1 required a perfect solution. The performance on each quiz guided the decision on the content of future quizzes. The results show that 15 quizzes were required to get 100% of the students to push through their difficulties and achieve expertise. The paper includes the content of the quizzes, the solutions, the aggregated results for each quiz, and the nature of the mistakes. It also includes an algorithm to conduct unit conversions and a visualization scheme to use tables of unit conversions and tables of metric prefixes that were developed during the project. These greatly assisted students in overcoming their difficulties. The experiment was repeated the following semester (Spring 2020, N=27) to test the effectiveness of an algorithm and visualization scheme developed by the author during the Fall 2019 semester. The time to achieve expertise was reduced to one third (5 quizzes vs 15 for the original group), thus confirming its merit. Part of the discussion section focuses on the benefit of the Scholarship of Teaching and Learning (SoTL) movement, of which this paper is an example, and its use in the ABET-required processes of outcomes assessment and continuous improvement. The paper also includes suggestions for further research.
Introduction
The process of learning units of measures, particularly unit conversions, seems rather painless when compared to the level of frustration students typically undergo while trying to master Newton’s laws of motion, the laws of thermodynamics, and the sequence of calculus courses, all of which are included in any ABET-accredited mechanical engineering undergraduate curriculum. The reason is because unit conversions only require low levels of math skills: simple knowledge of multiplication and division, along with addition and subtraction in some cases, such as converting temperature units. Most engineering faculty expect students to absolutely master unit conversions due to its apparent lack of difficulty and because unit conversions are taught in high school. However, in the author’s experience, students do not master this skill. Although there is little research into the nature and extent of the struggles with units, all the available literature points to a pervasive problem that plagues engineering curricula, including senior students. The literature review section summarizes these findings.
The lack of mastery of units of measure is worrisome given the fundamental and critical nature that units play in engineering projects. Mistakes with units are often grave and costly as evidenced by, for example, the loss of the $125 million NASA Mars Climate Orbiter spacecraft in 1999 [1]. One team in the project used English units of measurement while the other team used the metric system for a key spacecraft operation. The spacecraft missed its intended orbit and disintegrated in Mars’ atmosphere. Similarly, in 1983 the fuel ran out midflight on an Air Canada Boeing 767 after a metric conversion error [2, 3]. The error was caused by a confusion between pounds and kilograms and the plane took off with less than half the expected amount of fuel. The error was combined with the fact that the fuel gauges of the plane were inoperative. The pilots, who knew of the problem, worked around it and took off anyways. Fortunately, the pilot was able to land the plane without casualties but with damages to the aircraft. Regulations now require that fuel gauges be functional before flying. The changes in regulations solved half of the problem. The other half, a potential mistake with units, is unfortunately still very much present.
It is also worrisome because, how can we expect students to master higher level engineering concepts if they exhibit a critical weakness in the most basic of the fundamentals? For example, students may be overwhelmed by the application of the ideal gas law in a thermodynamics course just because they are not able to input values with consistent units. Although the math is relatively simple (Algebra I level), ensuring that the units are consistent is apparently more difficult than many people would think.
Viewed from a different perspective, this worrisome state may be turned into an excellent opportunity to conduct a wide variety of educational research projects on units of measure. Units combine both math and science and it does so at a relatively elementary level. Therefore, the difficulties in weaving together math and science can be explored at a level that is not very complicated. The science issues arise from the fact that the values obtained from scientific formulas (or measurements) are meaningless without units. Even if a quantity is non-dimensional, such as the Reynolds number used in fluid mechanics, it is still crucial for an engineer or scientist to know that the quantity is a pure number with no units attached to it. When examined from a math perspective, the process of converting units is a straightforward mathematical operation at the Algebra I level. The potential gain from resolving this issue is immense because, if solved early, students could enjoy a much richer educational experience. Students may still earn a few low grades in some courses due to the difficulty of the topics, but in terms of units, the students’ performance should always be impeccable.
This paper documents an experiment conducted in the Fall 2019 semester that focused specifically on the skill of converting units. No context nor applications were provided. Students were simply given a quantity with specified units and were told to convert the quantity to another unit; for example, convert a speed of 65 miles per hour to meters per second. The objective was to isolate the skill of conversion of units (straightforward math skill) from other skills related to science such as a unit check of a specific formula. The students were mechanical engineering seniors enrolled in a required training course for the NCEES Fundamentals of Engineering Exam (FE Exam). The FE Exam only allows a calculator and a 250-page reference handbook [4]. The handbook includes a table of metric prefixes (p. 1) and a table of unit conversions (p. 2). As the page numbers suggest, the examinees must master the fundamental skill of using metric prefixes and converting units before all others, if they expect to pass the FE Exam. The methodology section provides the full details of the experiment.
The experiment was repeated the following semester (Spring 2020) to test the effectiveness of a conversion algorithm and a visualization scheme for tables of unit conversions and tables of metric prefixes. These were developed in the process of trying to assist students in achieving expertise and are presented in the Methodology section. Results for both are included.
This paper includes the following sections: Abstract, Introduction, Research Questions, Literature Review, Methodology, Results, Discussion, Limitations, Further Research, and Conclusions.
Research Questions
- What is the extent of the struggles with unit conversions of mechanical engineering seniors enrolled in the course ENGI 478 Fundamentals of Engineering (Fall 2019)?
- What is the nature of the mistakes made by students while converting units?
- Can 100% of the students achieve mastery at converting units before the end of the semester? If so, how long does it take?
- [Add on question after obtaining the results of the Fall 2019 semester.] If the conversion algorithm and visualization scheme of tables of conversions developed in the Fall 2019 semester are presented on the first day of class of the Spring 2020 semester (during the discussion of the first quiz), will it reduce the time to achieve mastery?
Literature review
Dorko and Speer (2015) [5] investigated unit use in computations of area and volume in a Calculus I course. It sampled N=198 students from a large public northeastern university in the USA. They found that 73% of the students gave incorrect units for at least one task.
Dorko and Speer also mention that there is little research into the nature and extent of students’ struggles with units or why they exist; therefore, most of the evidence of the struggles is anecdotical. They cite four studies that evidence student difficulties with units in differential equations, physics and chemistry.
Redish (1997) [6] explores several aspects of student difficulties with math in the context of physics. Redish recognizes that students tend to want to put numbers into equations right away thus losing the possibility of doing unit checks for consistency (p. 10). On a similar line, Redish also points out the failure of many students to be able to parse equations, i.e., the ability to subdivide an equation into parts, to identify each of the parts, and to figure out their relations to each other. Therefore, if a student does not understand the equation immediately, they have no way of figuring out how to read it (p. 13). Also, many students fail to understand the role of mathematics as representing physical relations (p. 23).
Rowland (2006) [7] explored difficulties with units in a differential equations class by using quizzes. Only a few students were able to realize that the units of each term in the differential equation had to be the same. Also, only a few students were able to determine the units of a proportionality factor in a simple equation. He recommends instructors to not take the units knowledge for granted and that units be included explicitly in instruction.
Saitta, Gittings and Geiger (2011) [8] report on an activity in a first-semester general chemistry course in which dimensional analysis was used as a tool to keep track of units and to guide students through calculations. The activity was motivated by their observations that many students have not mastered unit conversions by the time they enter college.
Mikula and Heckler (2013) [9] conducted extensive testing and interviews of sophomore, junior, and senior engineering students at The Ohio State University and found that students struggle with many “essential skills” that were prerequisites, and that little to no instruction time was spent on them. Among these skills were dimensional analysis, using metric prefixes for various conversions, and operating equations when given variables in mixed units. They conducted an online training activity that, except for interpreting log plots and log scales, saw “little and insufficient improvement as a result of training, despite the basic nature of the skills”.
Dincer and Osmanoglu (2018) [10] administered a 14-question exam to n=73 prospective science teachers to examine their knowledge with unit conversions. The exam covered metric units for length, area, volume and mass. The findings indicated that “the performance was not satisfying in general”. They also report that the major difficulties were related to the metric prefixes, i.e., converting gram to microgram, dm3 into mm3, etc.
Nguyen and Rebello (2011) [11] uncovered difficulties with units while conducting an experiment to determine the specific types of difficulties students might have with different kinds of representations of classical mechanics problems. The representations were of three types: all numerical, numerical and some graphical information, or numerical and some functional relationship. The issue of using wrong units was categorized as “Difficulty with physical quantities” in the article (p. 561). The authors do not delve deeply into the difficulties with units in this article since their objective was to only develop a panoramic view of the difficulties.
Although the number of articles is limited, all of them, without exception, clearly show that many students are confronting difficulties with units. It is a pervasive problem in STEM education. This paper aims to fill a gap in the literature by looking at the extent and nature of the mistakes, and by striving to get 100% of the students to push through their difficulties and achieve mastery in converting units.
Methodology
The experiments took place in ENGI 478 Fundamentals of Engineering, a required course for all mechanical engineering students at a private university in the Central-East region of Puerto Rico. The goal of the course is to train students to pass the NCEES Fundamentals of Engineering Exam (FE Exam). The number of participants was N = 21 (Fall 2019) and N=27 (Spring 2020). The author is the instructor of the course.
In the Fall of 2019, a quiz on unit conversions was given at the beginning of each class, starting on day one of the semester. The students’ performance in the first quiz provided a first glimpse at the answer to research question 1 (what is the level of mastery of students in converting units?). The total number of quizzes and their exact content was not preordained because it depended on the third research question (how long does it take for all students to achieve mastery?). The students were told that daily quizzes would stop once 100% of the students showed mastery of conversion of units. In terms of the quiz content, the performance in previous quizzes guided the decision on the content of future quizzes. This freedom allowed the author to focus on observed areas of difficulty (for example, the use of metric prefixes) and train the students until they resolved the issues.
A total of 15 quizzes, presented in Table 1, were required to achieve mastery of unit conversions. The procedure consisted of writing the quiz question on the whiteboard at the beginning of class and students answered it individually in their notebooks. The score on the quiz was either one or zero, which simulated the FE Exam methodology of not awarding partial credit. To earn a score of 1, the performance had to be perfect and the quiz completed within 3 minutes, which is the average time required to solve an FE Exam problem. The author walked around the classroom, observed what each of the students was doing, and scored the quiz on the spot. The author then solved the problem on the whiteboard and discussed errors he had observed while walking around the classroom. The entire sequence of events took approximately 15 minutes per quiz. The solutions to the 15 quizzes are given in Table 2.
The second experiment (subsequent semester, Spring 2020) used the same quizzes.
The author presented the process of conversion of units as a systematic algorithm that ensures consistency and reduces the potential for errors. The steps for the algorithm are explicitly shown below in Table 3. The steps are described in the left column and an example is provided on the right column (convert 40 ft/s to m/s). The solutions to the 15 quizzes shown in Table 2 use the algorithm.
Results
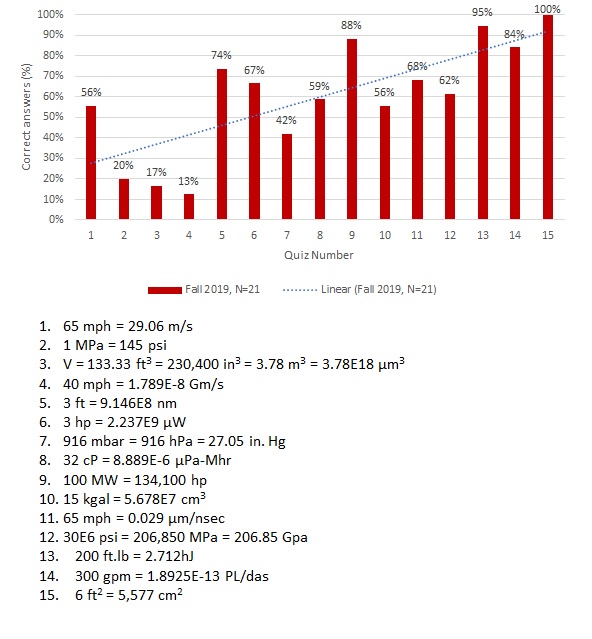
The results of the quizzes are provided in Fig. 1. The horizontal axis represents each of the 15 quizzes. The vertical axis provides the percentage of students that answered the question perfectly. The figure also includes a trend line (dotted blue line) which is a linear regression calculated with Excel. The legend includes the answers to all the questions as a quick reminder of the quiz content. Table 4 summarizes the errors committed by the students.
Fig. 1. Students’ performance in the 15 quizzes required to achieve expertise (Fall 2019)
Tab
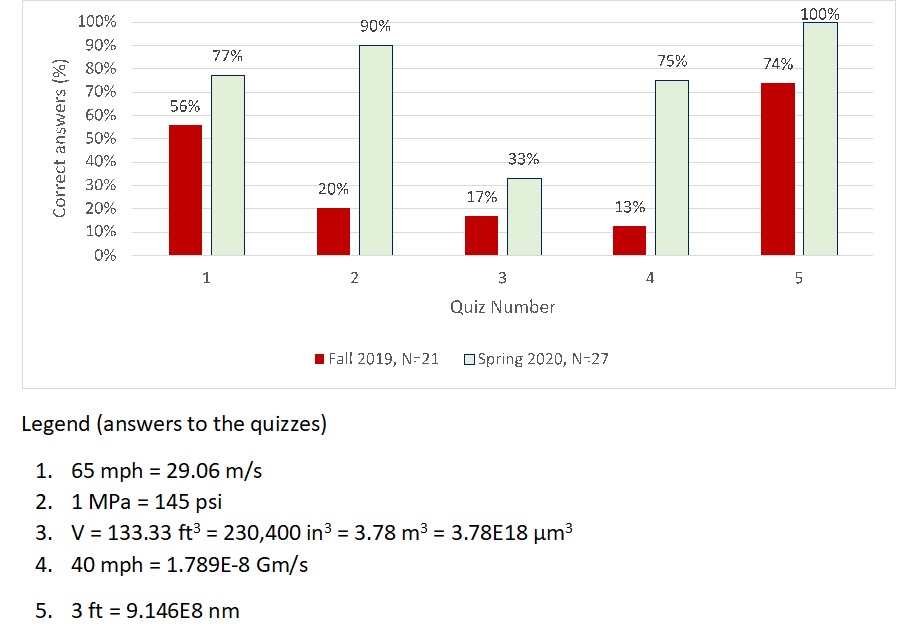
The results for the second experiment conducted the subsequent semester (Spring 2020) are shown in Fig. 2. The Fall 2019 group results are also shown to facilitate the comparison.
Fig. 2. Spring 2020 students’ performance in the 5 quizzes required to achieve expertise. The results of the Fall 2019 group are included to facilitate a comparison between the two groups.
Discussion
(Fall 2019 Group) Experience throughout the 15 quizzes
In general, the trend line in Fig. 1 shows that the performance improved with respect to time. There were some issues throughout the experience but, by the last three quizzes, almost everyone had mastered the skill. Perfection was achieved in the last quiz (#15). The issues experienced throughout the 15 quizzes are discussed below.
The response to Q1, the first quiz (convert 65 mph to m/s), immediately diagnosed that students were struggling with units. Only 55.6% of the students were able to answer Q1 correctly. In addition, seven of the eleven error types were committed in this first quiz (the first 7 items in Table 4). With respect to the first research question (the extent of the struggle), the answer is that approximately 50% of the students in this class struggled with units in the first day of class.
Q2 (convert 1 MPa to psi) was selected because it included the two preferred units for “stress” (MPa and psi), as used in machine design. Q2 was also the first instance in which the use of metric prefixes was required. The performance dropped to 20% and uncovered the issue of struggles with metric prefixes (see items 8, 9 and 10 in Table 4).
Q3 delved deeper into the nature of the potential errors by requiring the conversion of volumetric units. The performance dropped even further to 16.7%. The most common error was that students did not cube the conversion factor (item 11 in Table 4). In addition, many students once again showed difficulties with the metric prefixes. The author observed that most students had difficulties in part 3d which required a conversion to cubic micrometers.
In Q4 (convert 40 mph to Gm/s) students were once again pressed to deal with the issue of metric prefixes. The response was the lowest during the semester: 12.5%. At this point, the author realized that a stronger intervention was required and taught consistency to students by visualizing the tables provided by the NCEES in a different manner. The different visualization scheme is provided later in the paper as figures 2 through 5.
Q5 (convert 3 ft to nm) was a turning point in students’ performance. It once again pressed them with the issue of metric prefixes and this time, 73.7% of the students answered correctly. The lecture on visualizing differently the NCEES tables seemed to influence students strongly. They started becoming consistent and systematic and, therefore, less error prone.
Q6 (convert 3 hp to μW) once again asked students to perform with metric prefixes but used units of power for the first time. The response was a more respectable, yet insufficient, 66.7% correct responses.
Q7 (convert 916 mbar to hPa and then to inches of mercury) included units of pressure used in weather reporting, familiar to all in Puerto Rico due to the frequent occurrence of hurricanes. Also, the hPa unit required the use of metric prefixes. Only 42.1% of the class answered it correctly. The drop in performance was mostly due to their inability to find a suitable factor to convert to inches of mercury. This is further discussed within item 2 in Table 4.
Q8 through Q12 continued pressing on the issue of metric prefixes with a variety of units used throughout mechanical engineering. Some quizzes required conversions into unusual units as a training exercise to ensure that they could convert units. The number of correct responses varied as can be observed in Fig. 1.
Q13 (convert 200 ft.lb to hJ) finally obtained a class response above 90% correct (94.7%). Q14 (convert 300 gpm to PL/das) dropped to 84.2% but, finally, in Q15 (convert 6 ft2 to cm2), a perfect response of 100% was achieved.
Tables in the NCEES Handbook
The tables provided in pages 1 and 2 of the NCEES handbook (metric prefixes and unit conversions, respectively) were confusing to students. Fig. 3 shows part of the unit conversion table, including the heading.
Fig. 3. Part of the conversion table given in NCEES handbook [4, p.2]. It includes the headings “Multiply”, “By”, and “To Obtain” which favors a left-to-right unit conversion and created some confusion.
The format of Fig. 3 is useful if one, and only one, left-to-right, direct conversion is required; for example, convert from joule to Btu. If the conversion direction is reversed, from right-to-left (Btu to joule), the examinee must first decipher that they need to divide instead of multiply. This does not seem complicated; however, it requires additional thought and creates a source for errors. Also, in cases in which more than one conversion step is required, this format does not line up properly with the algorithm for converting units presented in Table 3.
It would be clearer and more useful to have a table that simply states the conversion as an equality, as shown below in Fig. 4.
Fig. 4. Proposed conversion table. It is very similar to Fig. 3 except that the number “1” has been added as a coefficient in front of all the units on the left column, and an equal sign has been placed between the two factors (both emphasized with ellipses). In addition, the potentially confusing column headings (“Multiply”, “By”, “To Obtain”) have been eliminated (compare to Fig. 3).
With Fig. 4, the only required decision is to determine which side of the conversion belongs in the numerator and which one in the denominator. The algorithm shown previously (Table 3) explains how to make this decision systematically to minimize the potential for errors. Also, although the coefficient “1” on the left column seems redundant, it is important to include it explicitly because it provides a magnitude. This lines up with the conversion algorithm which requires that the unit itself and its magnitude be treated separately (see Table 3).
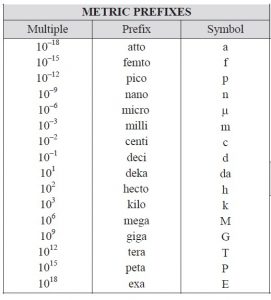
The table of prefixes in page 1 of the NCEES handbook may also be similarly improved to minimize the potential for errors. Fig. 5 shows the entire table as it is presented in the handbook. It gives the multiple, the prefix and the symbol. It is valuable information, but students continually made mistakes while using it. It can be easily improved by treating the multiples as conversion factors. Fig. 6 shows such a proposed table. It contains the same information as Fig. 5 but organizes it differently. Fig. 6 is also consistent with Fig. 4 (unit conversions) by having the coefficient “1” on the left side of the equality, and the multiplier as the coefficient on the right side. This consistency in presenting the information was shown to minimize the probability of erring in such a fundamental issue.
Fig. 5. Metric prefixes table given in the NCEES Handbook [4, p.1]. It contains all the necessary information; however, many students were not able to use it correctly.
Fig. 6. Proposed table of metric prefixes. The multiples are presented as conversion factors, so it is analogous to Fig. 4. This visualization scheme assisted students in overcoming their difficulties.
(Spring 2020 Group) Experience throughout the 5 quizzes
Fig. 2 shows the results of the second experiment. The objective was to answer research question 4, i.e., if the algorithm and visualization scheme are discussed in class after the first quiz, will it shorten the time to achieve mastery?
The results show that the time was shortened to one third (5 quizzes vs 15) which is very encouraging. The Spring 2020 group was bigger (N=27 vs N=21) which is even more promising for the algorithm and the visualization scheme of the tables. The improvement in quiz 2 was particularly significant because 90% (vs. 20% in Fall 2019) of the students correctly handled metric prefixes. This quiz was the first one after discussing the visualization schemes (Figs. 4 and 6).
However, the results of the first quiz for the Spring 2020 group (77% correct) was significantly higher than the Fall 2019 group (56% correct) which implies that it could be a “better” group of students. This may have had an influence in shortening the time to achieve mastery. Nevertheless, the consistency involved in using the algorithm and the visualization of the schemes appears to be a step in the right direction for achieving expertise.
Time to cover the syllabus
It has been made clear that students overcame their difficulties by providing proper training; however, there was a downside to conducting this research project. The time that was spent on the 15 quizzes, and briefly discussing them in class, contributed to a reduction in the amount of material covered in class. Assuming each intervention consumed 15 minutes on average, the total amount of time diverted was equal to 225 minutes (3 hours and 45 minutes). This is equivalent to 8.33% of a typical 45-hour semester course. The third research question was answered but it came at the cost of covering less material. (Can 100% of the students achieve mastery at converting units before the end of the semester? Yes. If so, how long does it take? 15 minutes of 15 class sessions for the Fall 2019 group and 15 minutes of 5 class sessions for the Spring 2020 group.)
The issue of “time to cover the syllabus” has been identified as a barrier to diffuse engineering education innovations in the classroom (Morales and Prince, 2019) [12] such as problem-based learning and project-based learning. This instance is no different. However, we must ask ourselves, is it worth it? The answer by this author is that it is certainly worth it if expertise can be achieved, as it was in this case. In the case of units, there is ample room to conduct the training at a much lower level, beginning at the high-school level and continuing in the introductory engineering courses. Students should master units before reaching this course.
Scholarship of Teaching and Learning (SoTL)
As a final discussion point, the project described in this paper is an example of the movement of Scholarship of Teaching and Learning (SoTL) in which post-secondary faculty approach teaching as a form of scholarly work with the goal of improving student learning and educational quality. SoTL starts with a question on student learning. The instructor must then determine how to address the question systematically through the teaching process. The University of Washington offers the following guidelines [13]:
Design: What have others done to address similar questions (literature review)? What assignments or other activities can help address your question?
Evidence: What indicators of student learning will be relevant for addressing your question? How can you systematically examine these learning indicators? How will you make sense of the student learning that you observe? How have others examined similar evidence of student learning?
Making it public: Who can provide an informed review or critique of your observations (of successes as well as failures)? How can you make your work available for others to adapt or extend (options include developing course portfolios for others to review, presenting at campus forums or conferences, and writing for publication)?
Using this paper as an application example of the guidelines given above: the “questions on student learning” that initiate the SoTL activity were posed as “Research Questions” in this paper; the literature review section includes what others have done, and revealed that the issue of units is a pervasive problem in STEM programs; quizzes were used as the “activity” that addressed the research questions; the results of the quizzes and direct observations were used as indicators of student learning; the process was made systematic by conducting a daily quiz until 100% of the students mastered the skill of unit conversions; the arguments made throughout this paper “make sense of the student learning” that was observed; this methodology has not been used previously, to the best knowledge of the author, but the literature review section includes the methodologies used by others; and finally, the results were “made public” through this publication. In addition, the publication will be shared with the faculty of the mechanical engineering program at this institution.
As a bonus, SoTL work offers a complementary deeper path to the outcomes assessment and continuous improvement processes required by ABET, in addition to typical processes which, unfortunately, tend to become perfunctory with time. At this university, SoTL was used for the first time last year to assess ABET outcomes “1” (complex problems), “2” (design – sizing), and “7” (acquire and apply new knowledge) based on a paper whose research questions revolved around the use of sizing existing machinery rather than an abstraction (a machine that is imagined) [14]. The main concept is that a real, existing machinery provides a “solution” against which the students (and faculty) can critically compare the sizing results. This allows students to gradually develop expertise before embarking on a creative major design experience (capstone).
The results of this paper will be used as a continuous improvement strategy to achieve compliance with ABET outcome “1” (complex problems). An expected continuous improvement strategy for the program is that units will be included explicitly in the learning objectives of several engineering courses (this was also a recommendation by Rowland [7]). The specific courses will soon be chosen by the entire faculty of the department.
Hopefully, these examples of SoTL will also provide motivation to the faculty to start using it in their courses.
Limitations
- The samples of the study were small (N=21 and N=27) which limits the generalizations that can be made. Nevertheless, the results line up with the literature finding that the lack of mastery of units is a pervasive problem in STEM education.
- The error types (Table 4) committed while converting units were not counted. In hindsight, this information would have been valuable to categorize the issues and analyze their frequency of occurrence.
Further research
The author offers the following ideas to continue research in this area:
- Continue the same activity in the same course to observe changes with respect to time (longitudinal study). The first quiz should be given as a “diagnostic quiz” to determine the level of expertise of the students on the first day of class. The discussion of the first quiz will include the conversion algorithm (Table 3), and the visualization schemes for unit conversions (Fig. 4) and metric prefixes (Fig. 6).
- Conduct the same SoTL research project in other engineering courses taught by other faculty members. This will allow the program to assess the effect of adding a specific learning objective related to units. It will also engage faculty in the SoTL movement. Also, the effects of this strategy should eventually be reflected in the course addressed in this paper (see first research idea above). The results could also be used to satisfy ABET Criterion 3 (outcomes assessment) and Criterion 4 (continuous improvement).
- Expand the scope by including conversions of mass. This paper did not include mass due to time constraints. Based on the author’s experience, and anecdotical evidence shared by colleagues in the department, the definitions of mass and weight, and the issues that revolve around them, are also an area of difficulty for students when applying them in Newton’s laws of motion, the first law of thermodynamics for open systems, the principle of impulse and momentum, and the calculation of moments of inertia of mass.
- Expand the scope by including “science” issues such as unit checks and dimensional analysis. These were not contemplated on the design of this project because the scope was reduced to the “math” issue related specifically to unit conversions.
- Expand the scope to include the science courses taught at the university level such as chemistry and physics. These are prerequisites to most of the engineering courses.
- Expand the scope by addressing high school teachers and students. The high school level is the stage in which units are seriously introduced. This research project could eventually lead to students that enter the university with much better skills.
Conclusions
The investigation described in this paper corroborates the findings in the literature that students struggle with unit conversions at a much higher rate than many people would think. The major observed difficulty in this study was the conversion of the metric prefixes, particularly the lack of a systematic and repeatable process that ensures flawless performance.
Approximately half of the group struggled in the first quiz. Still, proper training remedied the eleven types of errors that were uncovered. By the 15th quiz, 100% of the students had mastered the skill of converting units. These results answer the three research questions posed at the beginning of the study.
The paper presented the algorithm that was taught to students (Table 3). It also proposed a format for conversion tables (Fig. 4), including metric prefixes (Fig. 6), which are consistent with the algorithm. This format greatly assisted students in overcoming their struggles. They were all able to acquire expertise.
The second experiment (Spring 2020 group) proved the benefit of the algorithm and the visualization scheme by reducing the time to achieve expertise to one third (5 quizzes vs. 15).
References
[1] CNN (1999). Metric mishap caused loss of NASA orbiter. http://edition.cnn.com/TECH/space/9909/30/mars.metric.02/. Retrieved November 17, 2019. [2] NYTimes (1983). Jet’s fuel ran out after metric conversion errors. https://www.nytimes.com/1983/07/30/us/jet-s-fuel-ran-out-after-metric-conversion-errors.html. Retrieved 17NOV2019. [3] Williams, M (2003), Flight Safety Australia. 27 (July-August 2003) “The 156-tonne Gimli Glider” (PDF). Retrieved February 3, 2020. [4] NCEES (2013). FE Reference Handbook, version 9.2. National Council of Examiners for Engineering and Surveying. [5] Dorko, A., and Speer, N. (2015). Calculus students’ understanding of area and volume units. Investigations in Mathematics Learning, 8(1), 23-46. [6] Redish (1997) http://www.physics.umd.edu/perg/papers/redish/talks/math/index.html. Retrieved February 1, 2020. [7] Rowland, D.R. (2006). Student difficulties with units in differential equations in modelling contexts. International Journal of Mathematics, Education, Science, and Technology. 37(5), 553-558. [8] Saitta, E. K. H., Gittings, M.J., & Geiger, C. (2011). Learning dimensional analysis through collaboratively working with manipulatives. Journal of Chemical Education, 88(7), 910 – 915.] [9] Mikula, B. and Heckler, A. (2013). The effectiveness of brief, spaced practice on student difficulties with basic and essential engineering skills. Proceedings – Frontiers in Education Conference. 1059-1065. 10.1109/FIE.2013.6684989. [10] Dincer, E. and Osmanoglu, A. (2018). Dealing with Metric Unit Conversion: An Examination on Prospective Science Teachers’ Knowledge of and Difficulties with Conversion. Science Education International, 29(3). [11] Nguyen, D. and Rebello, N. (2011). Students’ Difficulties With Multiple Representations in Introductory Mechanics. US-China Education Review, ISSN 1548-6613 May 2011, 8(5), 559-569. [12] Morales, J.C., and Prince, M.J. (2019). Promoting Lasting Change in Teaching Practices Through a Summer Immersion Faculty Development Program. International Journal of Engineering Education, Vol. 35, No. 3, pp. 968–985. [13] Scholarship of Teaching and Learning (SoTL). https://www.washington.edu/teaching/programs/teaching-and-learning-symposium/scholarship-of-teaching-and-learning/. Retrieved February 24, 2020. [14] Morales, J.C (2019). Sizing the components of existing machinery to gradually develop machine design expertise. Proceedings of the 126th American Society of Engineering Education (ASEE) Annual Conference and Exposition. Tampa, Florida. June 16-19, 2019.
Trackback from your site.